
こんにちは、元塾講師のTanaです。
今回は「高校受験にむけ難問でおすすめの計算問題集が知りたい」という疑問に応えます。
次の家庭へおすすめの内容となります。
- 高校受験に不安を感じる
- 計算問題の難易度が高くて苦手意識を持っている
- 難問に対する十分な対策をしたいと考えている
高校受験を控える生徒や保護者の皆さんにとって、難問計算問題にしっかりと対策することは重要です。

数学の計算問題は、受験において特に重要な要素の一つであり、
その難易度は高校受験の合否を左右することもあります。
そこで、この記事では、高校受験に向けて難問を克服するためのおすすめ計算問題集を7つ紹介します。
これらの問題集は、幅広い難易度や問題形式を網羅し、生徒たちが計算力や問題解決能力を高めるのに役立ちます。
高校受験にむけ難問対策できる7つのおすすめ計算問題集

デジタル教材すらら
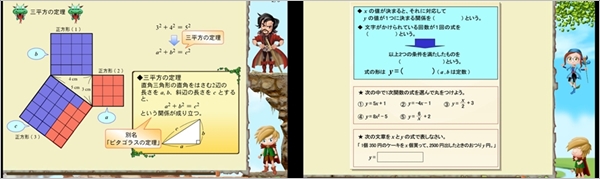
すららのおすすめ理由
通信教育サービス「すらら」は、高校受験における計算問題対策において非常に有益。
なぜなら「すらら」は難問に焦点を当てた問題集を提供しており、これによって受験生が高校入試に必要な計算力を養うことができるからです。
まず「すらら」の問題集は、高校受験で出題される計算問題の幅広い範囲をカバー。これにより受験生は基本的な計算力だけでなく、応用力や論理的思考力も養うことができます。また難関校を目指す受験生にとっては特に有益であり、しかもインターネット特性を活かした膨大な情報量で、高度な計算問題にむけた徹底対策が可能です。
さらに「すらら」は通信教育なので、受験生は自宅で自分のペースで学習することが可能。これは、忙しい生徒や地理的な制約がある生徒にとって非常に便利。また、難問に取り組むための時間や余裕を確保することができます。
加えて「すらら」の問題集は徹底した解説が付属しています。
これにより受験生は問題の解き方や計算のコツを理解し、自らの計算力を向上させることができます。また解説には難問に対するアプローチや解法が詳細に記載されており、高度な計算問題にも自信を持って取り組むことができます。
すららのおもな口コミ
- 支援級から普通級へのステップアップを果たし、すららの学習と過去問対策によって合格を勝ち取りました。
- 毎月40時間以上の学習時間を確保し、英検3級1次試験に合格しました。
- 基礎固めに力を入れたさかのぼり学習の結果、定期テストの点数を3割アップさせ、高校入試に合格しました。
- コロナ禍における先取り学習の成果として、中学最初のテストで100点を獲得しました。
- すららコーチのサポートを受けてテストの点数を20点以上向上させました。

以上のように「すらら」は高校受験における計算問題対策において、幅広い問題の提供、自宅学習の柔軟性、そして詳細な解説という点で非常に有益です。これにより受験生は難問にも臆することなく挑戦し、高校受験における計算力を確実に向上させることができます。
 ✅ こちらから「無料体験」ができます。
✅ こちらから「無料体験」ができます。
参考:通信教育すららの口コミレビュー「高校受験への対応力」を徹底検証
進研ゼミ「ハイレベルコース」
 出典:進研ゼミ
出典:進研ゼミ
進研ゼミのおすすめ理由
進研ゼミの「ハイレベルコース」は、高校受験に向けた難問の計算問題対策に非常に有益です。
まず「ハイレベルコース」は難関レベルの計算問題を豊富に提供しており、受験生が高校受験に必要な高度な計算力を養うことができます。
このコースでは、高校受験で出題される難問を中心に構成。そのため受験生は実際の受験問題に近い形式の問題に取り組むことができ、本番に近い状況での学習が可能。また難問に対する充分な対策を行うことで、受験時に自信を持って問題に臨むことができます。
さらに、「ハイレベルコース」は、専用タブレットや紙教材のどちらも選択可能。
これにより、受験生は自身の学習スタイルや環境に合わせて最適な学習方法を選択することができます。タブレットを使用することでインタラクティブな学習が可能になり、計算問題への理解をより深めることができます。
また「ハイレベルコース」はスタンダードコースと比べて難易度が高く、より高度な計算問題に取り組むことが求められます。このため受験生は計算力を向上させるだけでなく、論理的思考や問題解決能力も養うことができます。
進研ゼミのおもな口コミ
- 進研ゼミのおかげで、子供が社会の暗記に苦手意識を持っていたのが克服できました。スキマ時間に取り組むことで点数が伸び、安心感が得られました。
- 子供が提出物を丁寧に仕上げるようになり、内申点が上がったことに驚きました。進研ゼミの学習方法が成果をもたらしていると感じます。
- 受験勉強の際、進研ゼミの教材が役立ちました。特に社会や理科の語呂合わせは効果的で、子供が興味を持って取り組めています。
- 進研ゼミの学習プランは、子供の志望校選びにも役立ちました。先輩の体験談や勉強方法が参考になり、子供が自信を持って受験に臨めました。
- 子供が入試本番で冷静に対応できたのは、進研ゼミの学習内容がしっかり身に付いていたからだと思います。安心して受験に臨むことができました。

以上のように、「進研ゼミ」の「ハイレベルコース」は、高校受験における難問の計算問題対策において、適切な難易度の問題提供や学習方法の選択肢の豊富さ、高度な計算力の養成という点で非常に有益です。これにより、受験生は自信を持って高校受験に臨むことができるでしょう。
 ✅ こちらから「無料の体験資料」がもらえます。
✅ こちらから「無料の体験資料」がもらえます。
参考:進研ゼミ中学講座の口コミ・評判など総合的に徹底レビュー!
Z会の通信教育
 出典:Z会の通信教育
出典:Z会の通信教育
Z会のおすすめ理由
Z会の通信教育は、高校受験に向けた難問の計算問題対策において非常に有益です。
高校受験において、数学や理科などの科目で難解な計算問題が出題されることが一般的です。これらの問題は、受験生に高度な論理思考と計算能力を要求します。
Z会の通信教育では「高校受験コース」「中高一貫校コース」を含む様々なコースが提供されており、その中で高校受験に必要な計算問題への対策を行うことができます。特に「中高一貫校コース」では、高度な計算問題が豊富に含まれており、受験生はこれらの問題に対する解法やアプローチを習得することができます。
さらにZ会の通信教育では専門の講師による解説や指導が提供されるため、受験生は計算問題に対する理解を深めることができます。また学習進度や理解度に合わせて学習を進めることができるため、個々の学習ニーズに合った対策が可能です。
Z会のおもな口コミ
- 問題の質が高く、難問に挑む力がついた!
- 理解していないと解けない問題が多く、集中力が高まった。
- 映像解説と練習問題が連動しており、わかったつもりにならない学習ができる。
- 丁寧な映像解説と添削指導により、一人ひとりに合わせた理解が得られる。
- 得意な科目を先取りしやすいシステムが魅力で、個々のニーズに応えてくれる。

これらの要素が組み合わさり、Z会の通信教育が高校受験に向けた、難問の計算問題対策に極めて効果的であるデジタル問題集と言えます。
 ✅ こちらから「入会・資料請求」ができます。
✅ こちらから「入会・資料請求」ができます。
→ Z会の通信教育
![]()
数学 難関徹底攻略700選(高校入試特訓シリーズ)
 出典:東京学参
出典:東京学参
数学 難関徹底攻略700選のおすすめ理由
- 難関校の数学・最新入試問題
この問題集は難関校の過去の入試問題や、難関校に匹敵する高度な内容を取り入れています。また、最新の入試問題を含んでいるため、受験生が最新の傾向や出題形式にも対応できます。 - 充実した解説の提供
問題集には、問題の2倍以上の充実した解説が収録されています。特に高校受験に向けた難問の場合、解法やアプローチが複雑であり、それらを理解することが重要です。解説が充実していることで、受験生は自分の解答を振り返りながら学習を進めることができます。 - 数学が苦手な人にも対応
この問題集は、数学が苦手な人にも対応するよう配慮されています。解答では基本的な考え方から説明され、問題によっては複数の解法が紹介されています。また図説も多く取り入れられており数学の問題を直感的に理解しやすくなっています。数学が苦手な受験生でも、問題集を通じて十分に理解を深めることができます。 - 模擬テストの提供
最後の章には、問題集で学んだ全範囲からの模擬テストが収録されています。模擬テストは受験対策において重要な要素であり、受験生が実際の試験と同様の環境で問題に取り組むことができます。また繰り返し挑戦することで時間内により高い点数を取るための戦略を身につけることができます。
数学 難関徹底攻略700選のおもな口コミ
- 難易度が高く、内容が充実しています。
- 基礎を理解した上で挑戦する問題です。
- 問題の質が非常に高いです。
- 難関高校受験には必要不可欠です。
- 挑戦のやりがいが十分にあります!

以上の理由から、この計算問題集は高校受験にむけた難問の計算問題対策として非常に有益であると言えます。受験生が高度な思考力と応用力を身につけ、高校受験における数学の難問に対応できるようサポートしています。
難関校受験対策 ハイレベル中学数学問題集
 出典:チャート研究所
出典:チャート研究所
難関校受験対策 ハイレベル中学数学問題集のおすすめ理由
- 難関高校入試に対応した実戦的な問題集
問題はランダム配列で構成されており1回5問の実戦テスト形式を採用。この形式は受験本番での問題に近い状況をシミュレートし、受験生が本番に向けて実戦的な勉強を行うことができます。また問題のレベルに応じて「標準」「発展」「難関」の3段階のコースに分かれており、受験生の実力に合わせた演習が可能です。 - 幅広いレベルの問題が掲載
問題集には、標準・発展・難関の3つのレベルに分かれた問題が掲載されています。標準コースは公立高校入試レベル、発展コースは中堅私立高校入試レベル、難関コースは難関国公立・私立高校入試レベルの問題が収録されています。 - 解答編の充実した解説
別冊解答編には問題の答えだけでなく、問題の考え方や詳しい解説が掲載されています。解答編に収録された解説は問題の解法やアプローチの過程を詳細に解説しており、受験生が難問に対するアプローチの仕方を身につけることができます。解法の過程を確実に押さえることで、受験生はより効果的に問題解決能力を向上させることができます。
難関校受験対策 ハイレベル中学数学問題集のおもな口コミ
- 成果がすぐに現れ、満足しています。
- 問題のバリエーションが豊富で、苦手な部分を選んで復習できるのが良いです。例題と練習問題の組み合わせも効果的です。
- 説明がとてもわかりやすいです。
- 解説と例題が非常に分かりやすく、理解しやすいです。
- 家庭教師からのおすすめで購入しましたが、予習に役立っています。

以上の理由から、この計算問題集は高校受験にむけた難問の計算問題対策として非常に有益であると言えます。受験生が実戦的な勉強を行い、幅広いレベルの問題に対応する力を身につけることができます。
実力判定テスト10 【数学 偏差値65】
 出典:東京学参
出典:東京学参
実力判定テスト10のおすすめ理由
- 実戦的な問題編成
この問題集は高校入試の準難関校の入試問題を研究し、実際のテストの形式に即した10回のテスト形式に編集されています。問題は偏差値58〜63の高校の受験生を対象にしており、平易な問題は少なく、比較的問題量も多く作成されています。このようなテスト形式での演習は、受験生が本番の入試に向けて実践的な対策を行うことができるため、高校受験において非常に有益です。 - 問題の難易度調整
第1回から第10回までのテストでは、回を重ねるごとに徐々に難しくなるように問題が編集されています。このような設計により、受験生は自身の実力を徐々に高めながら、高校受験に向けての準備を進めることができます。また使いやすい解答用紙も付属しており、受験生がスムーズに演習を行うことができます。 - 解答・解説編の充実
解答・解説編には、各回のテストの解答だけでなく、解説も含まれています。これにより受験生は自身の解答を振り返りながら、問題の解法やアプローチの理解を深めることができます。また、解答・解説編には、合格判定の方法や学習の進め方も示されており、受験生が自己診断を行いながら効果的な学習を進めることができます。
実力判定テスト10のおもな口コミ
- 成果がすぐに現れ、満足しています。数学的な考え方の幅を広げてくれます。
- 高校入試向けとしては、1回あたりの問題数が少ないので、この問題集に慣れてしまうと危険ですね。
- 埼玉県立高校入試対策に最適です!よく出る少し発展的な問題が網羅されています。
- 私立高校入試には最適です。特に難関私立高校の入試問題としては最適です!
- もう少し難易度の高い問題集を選んだ方が良かったかもしれません。

以上のように、この計算問題集は高校受験にむけた難問の計算問題対策に非常に有益です。受験生が実際の入試に即した演習を行いながら、自身の実力を高め、合格への道を着実に進んでいくことができます。
数学 ハイクラステスト
 出典:受験研究社
出典:受験研究社
数学 ハイクラステストのおすすめ理由
- 3段階式でレベルアップ
この問題集は、標準レベル、応用レベル、難関レベルの3段階式で問題が構成されています。このような構成により、受験生は自身の実力に合わせて段階的に問題に取り組むことができます。また、1・2年の復習から始まり、次第に高度な問題に挑戦することで、高校受験に必要なスキルや知識を着実に身につけることができます。 - くわしい解答・解説
解答編には、正解だけでなく、詳細な解説や解き方が記載されています。この解説により受験生は難問でも理解しやすくなっており、自己学習においても効果的に活用できます。また注意すべきポイントや補足も付属しており、受験生が問題に取り組む際の手がかりとなります。 - ハイクラステストの特徴
ハイクラステストは、標準から応用、そして難関までの3段階に分けた問題構成が特徴。これにより、受験生は自身のレベルに合わせて段階的にステップアップできます。また国公立・私立難関校の入試問題から良問を精選しているため、実際の入試に即した対策が可能です。
数学 ハイクラステストのおもな口コミ
- 問題の量もちょうど良いです。公立高校の難関を目指す人は、この問題集を目標時間の7割から8割で完璧に解けるまで取り組むことで、十分な準備ができると思います。
- 来春、受験を控えた中学3年生ですが、難しい問題もあり少し大変ですが、とても勉強になります。
- 面白い問題がたくさんあります。

以上のように、この計算問題集は高校受験に向けた難問の計算問題対策に非常に有益です。受験生は段階的に問題に取り組みながら、必要なスキルや知識を効果的に身につけ、合格に向けて着実に準備を進めることができます。
高校受験にむけ難問の計算問題を解くコツ


高校受験の難問の計算問題を解くためには、いくつかのコツがあります。
以下にいくつかのアドバイスをまとめました。
問題を読み込む
高校受験の計算問題では、問題文を正確に理解することが重要です。問題文を読むときは、以下の点に注意してください。
- 何が求められているかを把握する
問題文の最後に「求められるもの」が明示されています。例えば、特定の数値や図形の寸法、あるいは問題の解法が求められることがあります。この部分を見逃さず、何を求められているかを確認しましょう。 - 与えられた情報を整理する
問題文中には、解くために必要な情報が含まれています。数値や条件、図形の特性などを整理し、それが問題の解法にどのように関連しているかを考えます。情報を整理することで、解法の手がかりを見つけやすくなります。 - 問題の文脈を理解する
問題文には、背景や条件が含まれています。例えば、物理学の問題であれば重力や摩擦といった物理法則が関連しています。文脈を理解することで、問題の要点を見極めることができます。
戦略を考える
問題解決には、様々な戦略があります。適切な戦略を選択するためには、以下の点に留意してください。
- 問題の性質を分析する
問題の種類や難易度、与えられた条件に応じて、適切な解法が異なります。例えば、代数的な方程式を解くべきか、図形の性質を利用すべきかを考えます。 - 既知の問題パターンを活用する
過去の問題や類題を解いてきた経験から、類似した問題に対する解法や戦略を思い出しましょう。類似性を見つけることで、問題解決の手がかりを得ることができます。 - 複数のアプローチを検討する
問題には複数の解法が存在することがあります。代数的なアプローチ、図形を用いたアプローチ、比較や割合を利用するアプローチなど、異なる視点から問題を考えてみましょう。
計算を丁寧に行う
計算ミスは解法を見つける上での大きな障害です。計算を丁寧に行うためには、以下のポイントに留意しましょう。
- 整数計算と小数計算を区別する
問題の性質に応じて、整数での計算が適切な場合と小数での計算が適切な場合があります。正確な答えが求められる場合は小数計算を、整数のみで十分な場合は整数計算を行いましょう。 - 途中経過を書き留める
計算を途中で記録することで、計算の過程を把握しやすくなります。間違いを見つけやすくなるだけでなく、誤りを見つけた際に修正するのも容易になります。 - 再確認を怠らない
計算が終了したら、答えを再度確認しましょう。解答が問題文の条件と整合しているかを確かめることで、誤りを防ぐことができます。
問題を分解する
複雑な問題を解く際には、問題を小さな部分問題に分解して解くことが役立ちます。
- 問題の構造を理解する
問題を解くためには、問題の構造を理解することが重要です。問題の要素や条件、関連性を把握し、問題を分解する際の手がかりを見つけます。 - 部分問題に分解する
問題を複数の部分問題に分割し、それぞれを解きます。各部分問題を解くことで、全体の解法を見つける手がかりを得ることができます。 - 部分問題の結果を統合する
各部分問題の解法や結果を統合し、全体の解法を導きます。部分問題ごとに得られた情報を繋ぎ合わせることで、最終的な解答を導きます。
反復練習する
難問の計算問題を解くためには、継続的な練習が必要です。
- 類題を解く
難問に取り組む前に、類似した問題や過去の問題を解いて練習します。類題を解くことで、解法や戦略を身につけることができます。 - 解答を確認する
解答を確認する際は、自分の解答と解答の違いや誤りを確認します。間違いを見つけた場合は、その原因を分析し、同じ誤りを繰り返さないようにします。 - 時間を意識して練習する
受験では時間が制約されますので、練習の際も時間を意識して取り組みます。時間内に解答を導き出すことができるよう、効率的な解法や計算のスキルを身につけましょう。
時計との競争
受験では時間が制約されますので、解く問題ごとに時間を意識して解答を進める練習が必要です。
- タイムマネジメントを行う
解くべき問題数や解答時間を考慮して、タイムマネジメントを行います。時間内にできるだけ多くの問題を解くために、問題ごとに解答にかける時間を調整します。 - スピードと正確さのバランスを取る
時間内に解答を導き出すことが重要ですが、正確な解答を得ることも同様に重要です。スピードと正確さのバランスを取りながら解答を進める練習を行いましょう。 - 時間配分を意識する
問題の難易度や解答にかかる時間を見極め、適切な時間配分を行います。時間を無駄にせず、効率的に問題を解くためには、時間配分の意識が重要です。
異なるアプローチを試す
問題解決には、異なるアプローチや視点から問題を見ることが重要です。
- 複数の解法を検討する
問題には通常、複数の解法が存在します。代数的なアプローチ、図形を用いたアプローチ、比較や割合を利用するアプローチなど、異なる解法を試してみましょう。 - 問題の条件を活かす
問題文に与えられた条件や情報を活かして、問題を解くアプローチを考えます。与えられた条件が解法に関連している場合、その条件をうまく活かすことが解法の鍵となります。 - 新たな視点を取る
問題に対して新たな視点やアプローチを試してみましょう。問題を別の角度から捉えることで、新たな解法や発見が得られる場合があります。

これらのアドバイスを実践しながら、高校受験の難問の計算問題に取り組んでください。継続的な練習と問題解決能力の向上を目指しましょう。
難問の計算問題でミスしやすい注意ポイント
細かな計算ミスに注意
- 指数や対数の計算
指数や対数の計算では、指数法則や対数の性質を適切に適用することが重要です。特に、指数や対数の加法や乗法、対数の底の変換など、細かい演算ミスが発生しやすい部分です。 - 三角関数の計算
三角関数の計算においては、角度の度数法と弧度法の混同や、特殊な角度における三角関数の値の間違いがよく見られます。また、三角関数の加法定理や積和公式を適用する際に、計算ミスが起こりやすいです。
問題文や条件の読み違いに警戒
- 複雑な問題文の読解
問題文が複雑で情報量が多い場合、重要な条件や求められていることを見落とす可能性が高まります。文字数や文章構造に惑わされず、要点を見極めるための読解力が必要です。 - 条件の見落とし
問題文や図形に与えられた条件が見落とされることがあります。特に図形問題では、図形や条件の関係性を十分に把握しないまま計算に入ると、誤った結論に至ることがあります。
適切な解法の選択に留意
- 解法の多様性への対応
高難度の問題では、一つの問題に対して複数の解法が存在します。解法の選択が問題の解答に影響を与えるため、問題の性質や自身の得意な手法を考慮して、最適な解法を選択する必要があります。 - 計算手順の体系化
計算問題においては、計算手順を体系的に整理し、段階的に進めることが重要です。具体的な手順を立てて、計算の途中で迷わずに正確に解答にたどり着けるよう工夫することが求められます。
高校受験で難問の計算問題が出題される学校の傾向


高校受験において、国立、公立、私立の学校で難問の計算問題が
出題される傾向にはいくつかの違いがあります。
国立高校の難問計算問題
国立高校の受験では、難問の計算問題が出題されることが一般的です。
国立高校は全国から志願者が集まり、競争率が非常に高いため、難易度の高い問題が用意されます。特に数学の計算問題は、高度な知識や論理的思考能力が求められるため、難問が多く含まれます。
これらの問題は、基本的な計算能力だけでなく、問題解決能力や応用力を測るために設計されています。

国立高校の数学の難問計算問題は、次のような特徴があります。
- 高度な問題設定
国立高校の数学問題は、複雑な問題設定が多いです。複数の概念やテクニックを組み合わせて解く必要があります。 - 応用力の試験
計算問題だけでなく、その計算結果を用いて新しい問題を解くことが求められることもあります。これによって応用力や洞察力が問われます。 - 精緻な計算が必要
演算ミスを防ぐために、正確で迅速な計算が求められます。計算の工程を逐一慎重に行うことが重要です。 - 論理的思考の重視
問題解決の過程で、論理的思考が不可欠です。問題の本質を見極め、適切な計算手法やアプローチを選択することが求められます。

これらの特徴を踏まえ、国立高校受験における数学の難問計算問題に対する対策は、幅広い問題に対する対応力や問題解決能力の向上が不可欠です。また、過去問演習や模擬試験を通じて、様々な問題形式に慣れることも重要です。
公立高校の難問計算問題
公立高校の受験でも、難問の計算問題が出題されることがあります。
公立高校の受験は、地域や学区によって異なるため、難易度や出題形式も多様です。しかし志願者同士の競争が激しいため、高難度の問題に対応できる力が求められます。

公立高校の数学の難問計算問題には、次のような特徴があります。
- 幅広い出題範囲
公立高校の数学問題は、幾何学や代数など様々な分野から出題されます。また、応用問題も多く含まれるため、幅広い知識と応用能力が求められます。 - 時間的制約
公立高校の受験は時間的にも制約があります。計算問題を迅速に解く能力が重要であり、時間を効率的に使う練習も欠かせません。 - 思考力の試験
問題解決の過程で、論理的思考や問題解析能力が問われます。問題の本質を見極め、適切な解法を選択する力が求められます。 - 応用問題の出題
実世界の問題をモデル化し、数学的手法で解決する応用問題が出題されることもあります。これによって応用力や発想力が試されます。

公立高校受験における数学の難問計算問題への対策は、過去問演習や模擬試験を通じて、様々な問題形式に慣れることが重要です。また、計算スピードを向上させるための練習や、論理的思考能力を養うための演習が必要です。
私立高校の難問計算問題
私立高校の受験でも、一部の難関私立高校では、高難度の計算問題が出題されることがあります。
これらの学校では、志願者数が少ないために難易度を高めることで、学力の高い生徒を選別する傾向があります。そのため、難問の計算問題に対する対策が必要です。

私立高校の数学の難問計算問題は、次のような特徴があります。
- 厳密な問題設定
私立高校の数学問題は、問題文や条件が複雑で厳密です。概念の理解と論理的思考が求められます。 - 応用問題の出題
現実の問題を数学的手法で解決する応用問題が出題されることがあります。問題解決能力や応用力を試す目的があります。 - 多様な問題形式
代数、幾何、確率など様々な分野から問題が出題されるため、幅広い知識と応用能力が求められます。 - 解答の厳密性
計算の過程や答えの精度について、厳密な解答が求められることがあります。演算ミスを防ぐためにも、正確な計算が重要です。

私立高校受験における数学の難問計算問題への対策は、基礎知識の徹底と論理的思考能力の向上が不可欠。
過去問演習や模擬試験を通じて、幅広い問題に対する対応力を養うことが重要です。また、計算スピードの向上や正確な計算の習慣化も重要です。
まとめ

高校受験における計算問題や難問に立ち向かう際、
この計算問題集は非常に有益です。
解答を通じて様々な計算手法や解法を習得し、難問に対する自信をつけることができます。
是非この問題集を活用して、高校受験での計算問題に備えましょう!


